Cos2x formula in terms of tan cos2x = 1 tan 2 x / 1 tan 2 x;In this video, I show how with a right angled triangle with hypotenuse 1, sides (a) and (b), and using Pythagoras' Theorem, thatcos(x) = 1 / sqrt( 1 tan^2 Tan2x Formula Sin 2x, Cos 2x, Tan 2x is the trigonometric formulas which are called as double angle formulas because they have double angles in their trigonometric functions Let's understand it by practicing it through solved example

How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic
Tan 2x formula in terms of cos x
Tan 2x formula in terms of cos x- There's a very cool second proof of these formulas, using Sawyer's marvelous ideaAlso, there's an easy way to find functions of higher multiples 3A, 4A, and so on Tangent of a Double Angle To get the formula for tan 2A, you can either start with equation 50 and put B = A to get tan(A A), or use equation 59 for sin 2A / cos 2A and divide top and bottom by cos² AThe trigonometric formulas like Sin2x, Cos 2x, Tan 2x are popular as double angle formulae, because they have double angles in their trigonometric functions For solving many problems we may use these widely The Sin 2x formula is \(Sin 2x = 2 sin x cos x\) Where x is the angle Source enwikipediaorg Derivation of the Formula



What Are The Formulas Of Cos 2x Quora
hmm, sin/cos=tan, cos/sin=cot, sin^2 cos^2=1 i need cos(theta) in terms of tan(theta) though Unless thats what we are working up to )Cos(x)^2(1tan(x)^2)=1 Replace the with based on the identity Simplify each term Pull terms out from under the radical, assuming positive real numbers The period of the function can be calculated using Replace with in the formula for period Solve the equation In Trigonometry Formulas, we will learn Basic Formulas sin, cos tan at 0, 30, 45, 60 degrees Pythagorean Identities Sign of sin, cos, tan in different quandrants Radians Negative angles (EvenOdd Identities) Value of sin, cos, tan repeats after 2π Shifting angle by π/2, π, 3π/2 (CoFunction Identities or Periodicity Identities)
If you're doing this by de Moivre, the trick is to keep the form you get from initially expanding (CiS)^3, (where C = cos x, S = sin x) rather than rewriting to get sin 3x in terms of only sin x ie (CiS)^3 = C^3 3i C^2S 3 C S^2 iS^3 So sin 3x =3 C^2 S S^3, cos 3x = C^33CS^2 And Then just divide by C^3 to rewrite in terms of tan xFormula to Calculate tan2x Tan2x Formula is also known as the double angle function of tangent Let's look into the double angle function of tangent ie, tan2x Formula is as shown below tan 2x = 2tan x / 1−tan2x where, tan x = Opposite Side / Adjacent Side tan 2x = Double angle function of tan x tan 2 x = Square funtion of tan x3x 2x = 5x is an identity that is always true, no matter what the value of x, whereas 3x = 15 is an equation (or more precisely, a conditional equation) that is only true if x = 5 A Trigonometric identity is an identity that contains the trigonometric functions sin, cos, tan, cot, sec or csc Trigonometric identities can be used to
The most straightforward way to obtain the expression for cos(2x) is by using the "cosine of the sum" formula cos(x y) = cosx*cosy sinx*siny To get cos(2 x ), write 2x = x xThe cosine of double angle is equal to the quotient of the subtraction of square of tangent from one by the sum of one and square of tan function cos 2 θ = 1 − tan 2 θ 1 tan 2 θ It is called the cosine of double angle identity in terms of tangent functionCos2x formula in terms of cos cos2x = cos 2 xsin 2 x;




Prove The Identity 2 Sin X Cos X Tan 2x 2 Chegg Com



What S The Integral Of Tan 2x Quora
Write tan(3x) in terms of tan(x) Hence show that the roots of t^3 3t^2 3t 1 = 0 are tan(pi/12), tan(5pi/12) and tan(3pi/4) The first part is relatively simpleSince both terms are perfect squares, factor using the difference of squares formula, where and Apply the tangent double angle identity Simplify the denominator The formula given in my book does not seem to work in Mathcad Prime 30 In the book there is no multiplier (*) printed after tan^2 and cos^2 There is just empty space I did change the formula around in all kinds of ways I put tan inside parenthesis like (tan)^2, or (tan^2* (gammaQ)), or (tan (gammaQ)^2) but nothing works




Powers Of Trigonometric Functions




Trigonometric Identity Challenge Sin 2 Cos 2x Tan 2x Youtube
Double angle formulas We can prove the double angle identities using the sum formulas for sine and cosine From these formulas, we also have the following identities sin 2 x = 1 2 ( 1 − cos 2 x) cos 2 x = 1 2 ( 1 cos 2 x) sin x cos x = 1 2 ( sin 2 x) tan 2 x = 1 − cos 2 x 1 cos 2 xCos 2x = (1tan^2 x)/(1 tan^2 x)` Plugging `tan x = sqrt6/3` in the formulas above yieldsThe functions sine, cosine and tangent of an angle are sometimes referred to as the primary or basic trigonometric functions Their usual abbreviations are (), (), and (), respectively, where denotes the angle The parentheses around the argument of the functions are often omitted, eg, and , if an interpretation is unambiguously possible The sine of an angle is defined
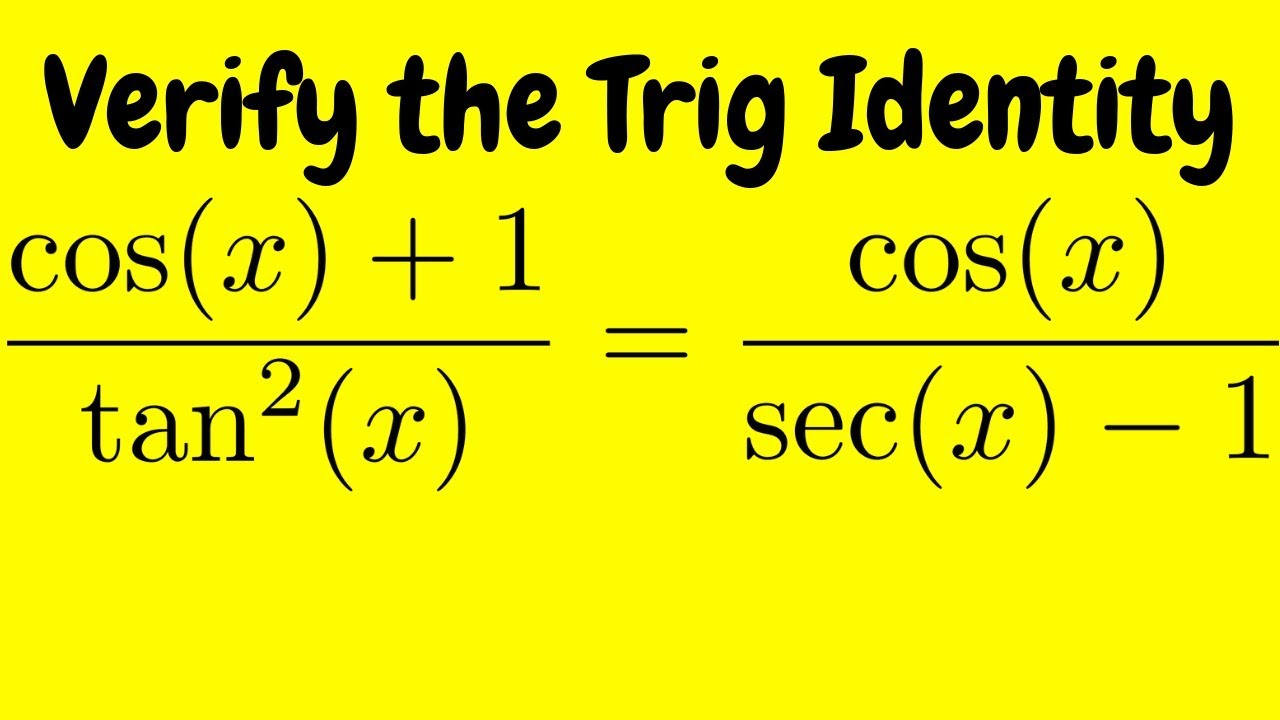



Verifying A Trigonometric Identity Cos X 1 Tan 2 X Cos X Sec X 1 Youtube




Solve Tan2x Cot X P 3 Brainly In
Tan2x Formulas Tan2x Formula = 2 tan x 1 − t a n 2 x We know that tan (x) = sin (x)/cos (x) cos2x = cos 2 xsin 2 x; Explanation using the trigonometric identities ∙ xtanθ = sinθ cosθ ∙ xsin2θ cos2θ = 1 ⇒ sinθ = ± √1 − cos2θ tanθ = sinθ cosθ = ± √1 −cos2θ cosθ Answer link




Write Cos2x In Tan And Prove Trigonometric Identity For Double Angle Youtube




How To Write Double Angle Formula Sin 2x In Terms Of Tan X Youtube
Cos 2A in Terms of tan A We will learn how to express the multiple angle of cos 2A in terms of tan A Trigonometric function of cos 2A in terms of tan A is also known as one of the double angle formula We know if A is a number or angle then we have, cos 2A = cos2 A sin2 A cos 2A = c o s 2 A − s i n 2 A c o s 2 A ∙ cos2 AFollow Report by Namrata9667 3Tan(3x) in terms of tan(x), write tan(3x) in terms of tan(x), using the angle sum formula and the double angle formulas, simplifying trig identities, trigono




1 Tan 2x 1 Cos 2x Sin 2x 2sin 4x 1 Sin 2x Trigonometric Identities Mcr3u Youtube
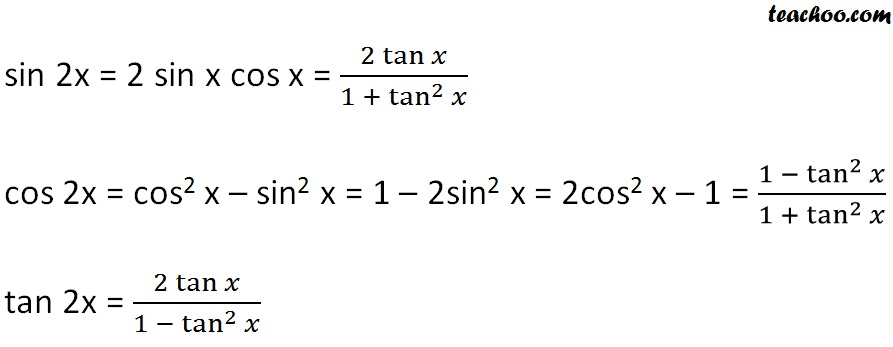



Half Angle Formulas Power Reducing Formulas 2x 3x Formula Provin
243 The Substitution z = tan (x/2) Suppose our integrand is a rational function of sin (x) and cos (x) After the substitution z = tan (x / 2) we obtain an integrand that is a rational function of z, which can then be evaluated by partial fractionsThe double angle formulas can be derived by setting A = B in the sum formulas above For example, sin(2A) = sin(A)cos(A) cos(A)sin(A) = 2sin(A)cos(A) It is common to see two other forms expressing cos(2A) in terms of the sine and cosine of the single angle A Recall the square identity sin 2 (x) cos 2 (x) = 1 from Sections 14 and 23$\tan^2{x} \,=\, \sec^2{x}1$ $\tan^2{A} \,=\, \sec^2{A}1$ In this way, you can write the square of tangent function formula in terms of any angle in mathematics Proof Take, the theta is an angle of a right triangle, then the tangent and secant are written as $\tan{\theta}$ and $\sec{\theta}$ respectively in trigonometry The mathematical




Misc 10 Sin X 1 4 Find Sin X 2 Cos X 2 Tan X 2 Chapter 3



If Cos X 1 2 Then What Is The Value Of Tan 2x Quora
Here is an approach using polynomials Write $\cos(2x)=\frac{1\tan^2(x)}{1\tan^2(x)}$ Double Angle Formulas The trigonometric double angle formulas give a relationship between the basic trigonometric functions applied to twice an angle in terms of trigonometric functions of the angle itself Tips for remembering the following formulas We can substitute the values ( 2 x) (2x) (2x) into the sum formulas for sin \sin sin andTan (2x) is a doubleangle trigonometric identity which takes the form of the ratio of sin (2x) to cos (2x) sin (2x) = 2 sin (x) cos (x) cos (2x) = (cos (x))^2 – (sin (x))^2 = 1 – 2 (sin (x))^2 = 2 (cos (x))^2 – 1 Proof 71K views View upvotes View shares
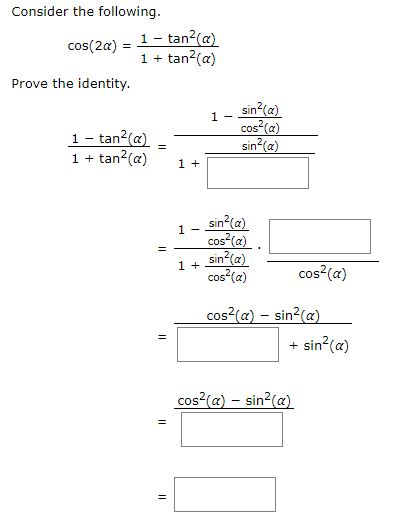



Prove The Identity 2 Tan X Sin 2x 1 Tan2x Write Chegg Com




Tangent Half Angle Formula Wikipedia
I wanted to find $\tan2x$ in terms of $\cos x$ alone I was able to do it in terms of $\sin x$ alone $\tan2x = \sin2x/\cos2x$ Since, $\cos2x = 12\sin^2x$ Therefore, $\tan2x = (\sin2x / 12\sin^2x)$ Is it possible to do it in terms of $\cos x$ alone ?• take the Pythagorean equation in this form, sin2 x = 1 – cos2 x and substitute into the First doubleangle identity cos 2x = cos2 x – sin2 x cos 2x = cos2 x – (1 – cos2 x) cos 2x = cos 2 x – 1 cos 2 x cos 2x = 2cos 2 x – 1 Third doubleangle identity for cosine Summary of DoubleAngles • Sine sin 2x = 2 sin xYou need to write sin 2x and cos 2x in terms of tanx such that `sin 2x = (2 tan x)/(1 tan^2 x);




Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com




Tangent Half Angle Formula Wikipedia
tan(x)=sin(x)/cos(x) 1tan 2 (x)=sec 2 (x) The Attempt at a Solution sin(x)=cos(x)tan(x) I don't think there is any way to express the sign just in terms of the tangent function because the tangent function has two periods for one for the cosine and sine You might be able to concoct a formula using greatest integer and mod functions toNow if you are wondering what the formula of cos2x is, let me tell you that we have 5 cos x formula The trigonometric formula of cos2x = Cos²x Sin²x The trigonometric formula of cos2x = 1 2Sin²x The trigonometric formula of cos2x = 2Cos²x 1 The trigonometric formula of cos2x = \\frac{1tan^{2}x}{1tan^{2}x}\Cos2x = 2cos 2 x1;




Ex 3 3 19 Prove Sin X Sin 3x Cos X Cos 3x Tan 2x




Trig Identity Tan X 1 Tan 2 X Sec X Cos X Csc X Sin X Proved From Both Sides Youtube
Sine, tangent, cotangent, and cosecant are odd functions while cosine and secant are even functions sin –t = –sin t cos –t = cos t tan –t = –tan t Sum formulas for sine and cosine sin (s t) = sin s cos t cos s sin t cos (s t) = cos s cos t – sin s sin t Double angle formulas for sine and cosine sin 2t = 2 sin t cos tGraph of Cos2x Integration of Cos2x The integral of cos2x = (1/2)sin(2x) C, Where C is constant Finding the integral of Cos(2x)Sin 2A in Terms of tan A We will learn how to express the multiple angle of sin 2A in terms of tan A Trigonometric function of sin 2A in terms of tan A is also known as one of the double angle formula We know if A is a number or angle then we have, sin 2A = 2 sin A cos A ⇒ sin 2A = 2 s i n A c o s A ∙ cos 2 A ⇒ sin 2A = 2 tan A ∙ 1 s e c 2 A
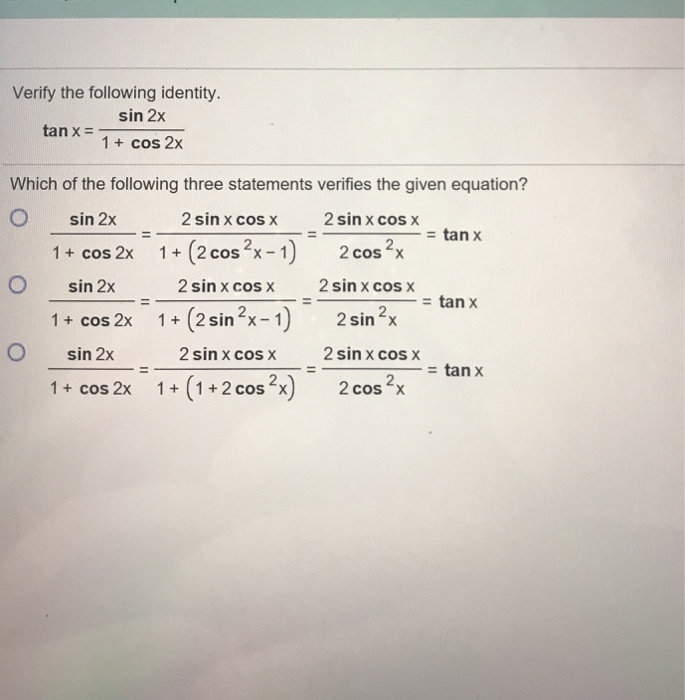



Verify The Following Identity Tan X Sin2x 1 Cos Chegg Com
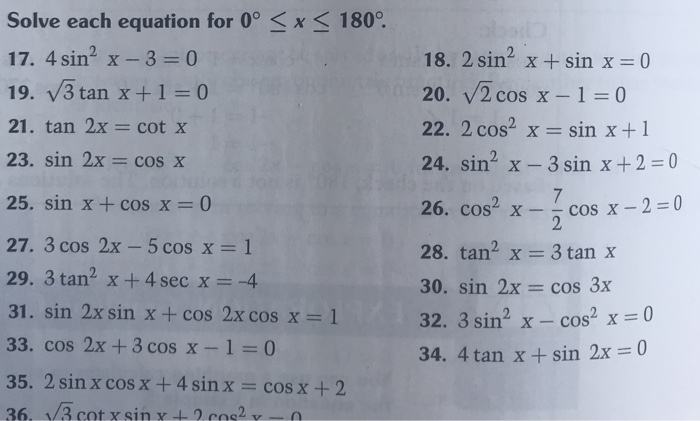



Solve Each Equation For 0 X 180 17 4 Sin2 Chegg Com
Let x 1(t) = A 1 cos(w 0t˚ 1), x 2(t) = A 2 cos(w 0t˚ 2), and x(t) = x 1(t)x 2(t) Then x(t) = Acos(w 0t˚) and the phasor representation for x(t) is X= Aej˚= A 1e j˚ 1 A 2e j˚ 2 ContinuousTime Unit Impulse and Unit Step Z 1 1 (t)dt= 1 Z 1 1 x(t) (t)dt= x(0) Z 1 1 x(t) (t t 0)dt= x\(\cos 2X = \cos ^{2}X – \sin ^{2}X \) Hence, the first cos 2X formula follows, as \(\cos 2X = \cos ^{2}X – \sin ^{2}X\) And for this reason, we know this formula as double the angle formula, because we are doubling the angle Other Formulae of cos 2X \(\cos 2X = 1 – 2 \sin ^{2}X \) To derive this, we need to start from the earlier derivationCreated by Sal Khan Exponential functions differentiation Derivatives of sin (x), cos (x), tan (x), eˣ & ln (x) This is the currently selected item Derivative of aˣ (for any positive base a) Practice Derivatives of aˣ and logₐx Worked example Derivative of 7^ (x²x) using the chain rule Practice Differentiate exponential functions




Example 1 Evaluate Trigonometric Expressions Find The Exact Value Of A Cos 165 And B Tan P 12 A Cos 165 1 2 Cos 330 1 Cos 330 2 Ppt Download



What Is The Formula Of Tan2x Quora
Simplify\\frac {\sec (x)\sin^2 (x)} {1\sec (x)} simplify\\sin^2 (x)\cos^2 (x)\sin^2 (x) simplify\\tan^4 (x)2\tan^2 (x)1 simplify\\tan^2 (x)\cos^2 (x)\cot^2 (x)\sin^2 (x) trigonometricsimplificationcalculator en State the formula of cos 2x in terms of tan x(state only ) cos 2x= 1 Log in Join now 1 Log in Join now Secondary School Math 5 points State the formula of cos 2x in terms of tan x(state only ) cos 2x= Ask for details ;So I'll have to use a formula Solve 3tan 3 (x) – 3tan 2 (x) – tan(x) 1 = 0 in full generality I can factor this in pairs When nothing looks like it's going to work, sometimes it helps to put everything in terms of sine and cosine That process, applied to this equation, gives me




Sec 6x Tan 6x 1 2 Tan 2x Sec 2x Important Difficult Trigonometric Identity Youtube




Cos2x Sin2x 1 1 Tan2x Sec2x Cot2x 1 Csc2x Cofunction
The double of the angle \(x\) is represented by the given formulas (i) \( \sin (2x) = (x) \cdot \cos (x) = \left {\frac{{2 \tan x}}{{(1 x)}}} \right\) (ii) \( \cos (2x) = – (x) = \left {\frac{{(1 – x)}}{{(1 x)}}} \right\) (iii) \( \cos (2x) = 2(x) – 1 = 1 – 2(x)\) (iv) \( \tan (2x) = \frac{{2\tan (x)}}{{1 – (x)}}\) (tanx cotx)^2=sec^2x csc^2x 3 cos(xy) cos(xy)= cos^2x sin^2y CALCULUS Please help ʃ (4sin²x cos²×/sin 2x cos 2x)dx That's integration of (4sin^2x cos^2x over sin 2x cos 2x) dx i've got it from the back and it has an answer from the back page of the book but i want to know how to solve iti I assume I need to convert #cot(x) tan(x)# into terms of cosine and sine, then end up with #1/(sin(x)cos(x))#, but I get stuck with how to deal with the rest of the problem from there Trigonometry Trigonometric Identities and Equations Solving Trigonometric Equations



Relating Trigonometric Functions Trigonometry Socratic
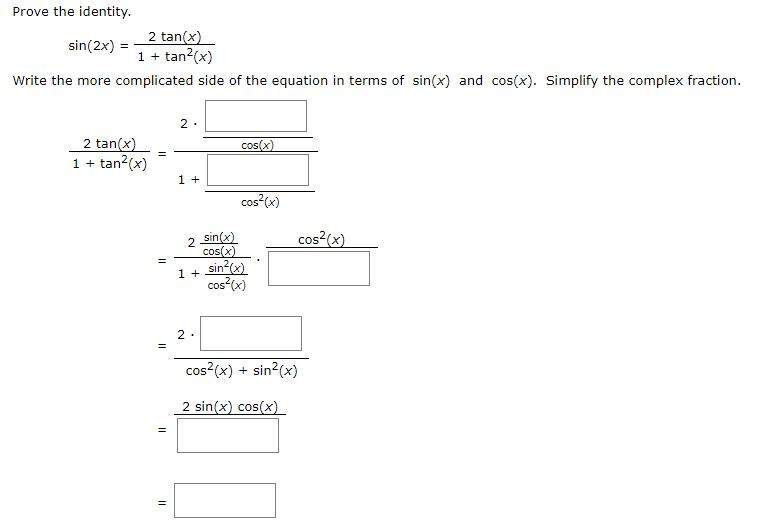



Prove The Identity 2 Tan X Sin 2x 1 Tan2x Write Chegg Com
We know from double angle formula that sin 2x = 2 sin x cos x = 2 tan x / (1 tan^2 x) cos 2x = cos^2 x sin^2 x = 1 2 sin^2 x = 2 cos^2 x 1 = 1 tan^2 x / 1 tan^2 x tan 2x = 2 tan x / (1 tan^2 x) These identities can also be used to reduce angles sin x = 2 sin x/2 cos x/2 = 2 t



3
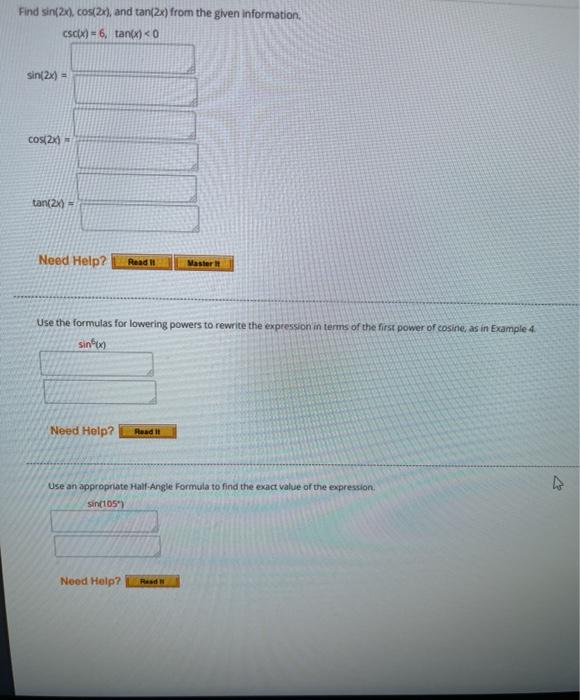



Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com




Ex 13 1 22 Lim X Pi 2 Tan 2x X Pi 2 Chapter 13 Class 11




How Does One Verify Cos 2x Sin 2x 1 Tan 2x Cos 2x Socratic




Tutorial Exercise Find Sin 2x Cos 2x And Tan 2x Chegg Com




Weierstrass Substitution Wikipedia
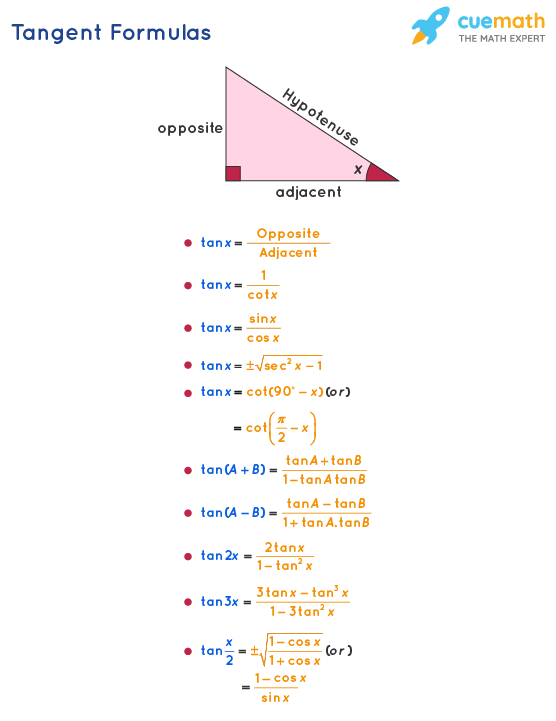



Tangent Formula What Are Tangent Formulas Examples



Classroomweb Pusd11 Net Sites Mmalmos Shared documents Precalculus honors Chapter 5 analytic trigonometry Hw ch 5 Pdf




Tangent Half Angle Formula Wikipedia




Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com
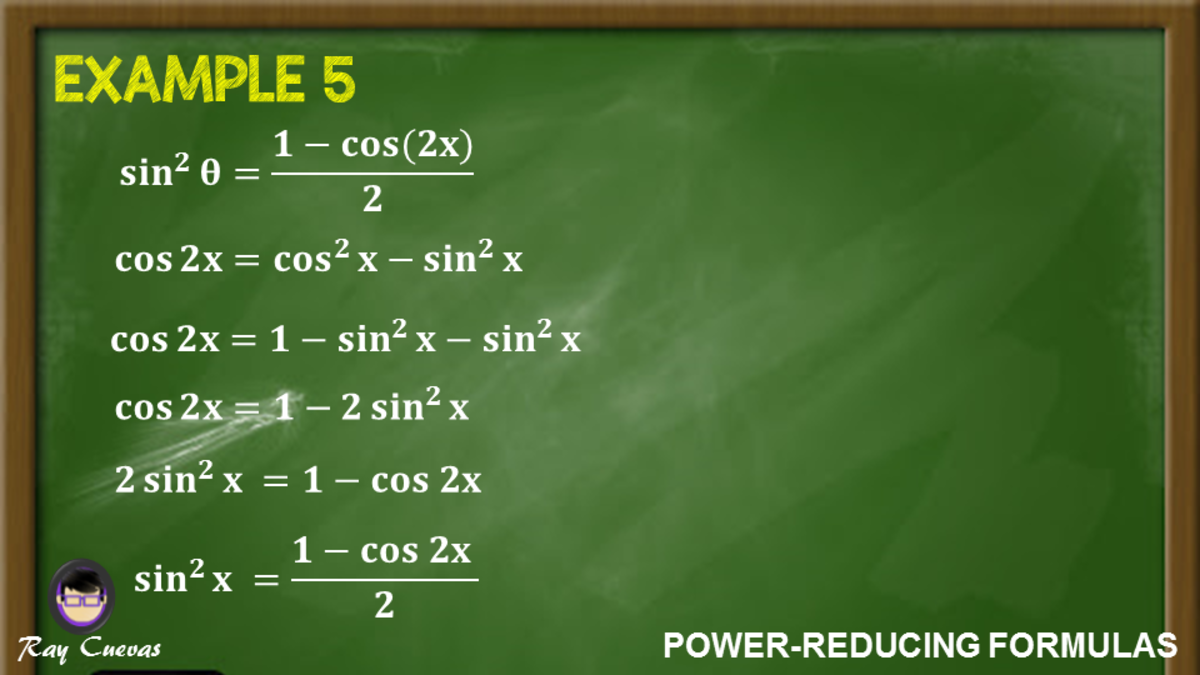



Power Reducing Formulas And How To Use Them With Examples Owlcation




Rewrite The Expression In Terms Of The First Power Of The Cosine Cos 4xtan 2x Brainly Com




Tan 2x Formula What Is Tan 2x Formula Examples




1 Tan 2x 1 Tan 2 X 1 2cos 2 X Youtube




Trig Identity Sec2x Minus Tan2x T10 Youtube




3 If Sin X Cos X 1 5 Then Tan 2x Is Equal To A 25 17 B 25 7 D 7 25 14 General Solution Of The Equation C 24 7




Solve The Following Equation Tan X Tan 2x Tan 3x 0




How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic




5 Tan 2x Cos 2x 2cos2x 9 Find Cos4x Iit Jee Trigonometry Double Angle Youtube




How Do You Find A Double Angle Formula For Sec 2x In Terms Of Only Csc X And Sec X Socratic



What Is The General Solution Of X For Tan X Tan2x 1 Quora




Write Cos2x In Terms Of Tanx Double Angle Transformation Youtube




Cos2xu003dcosx
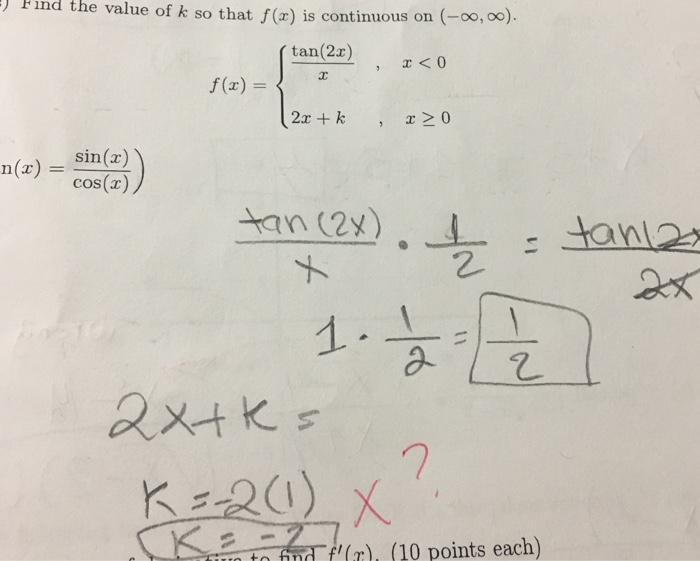



Find The Value Of K So That F N Is Continuous On Chegg Com
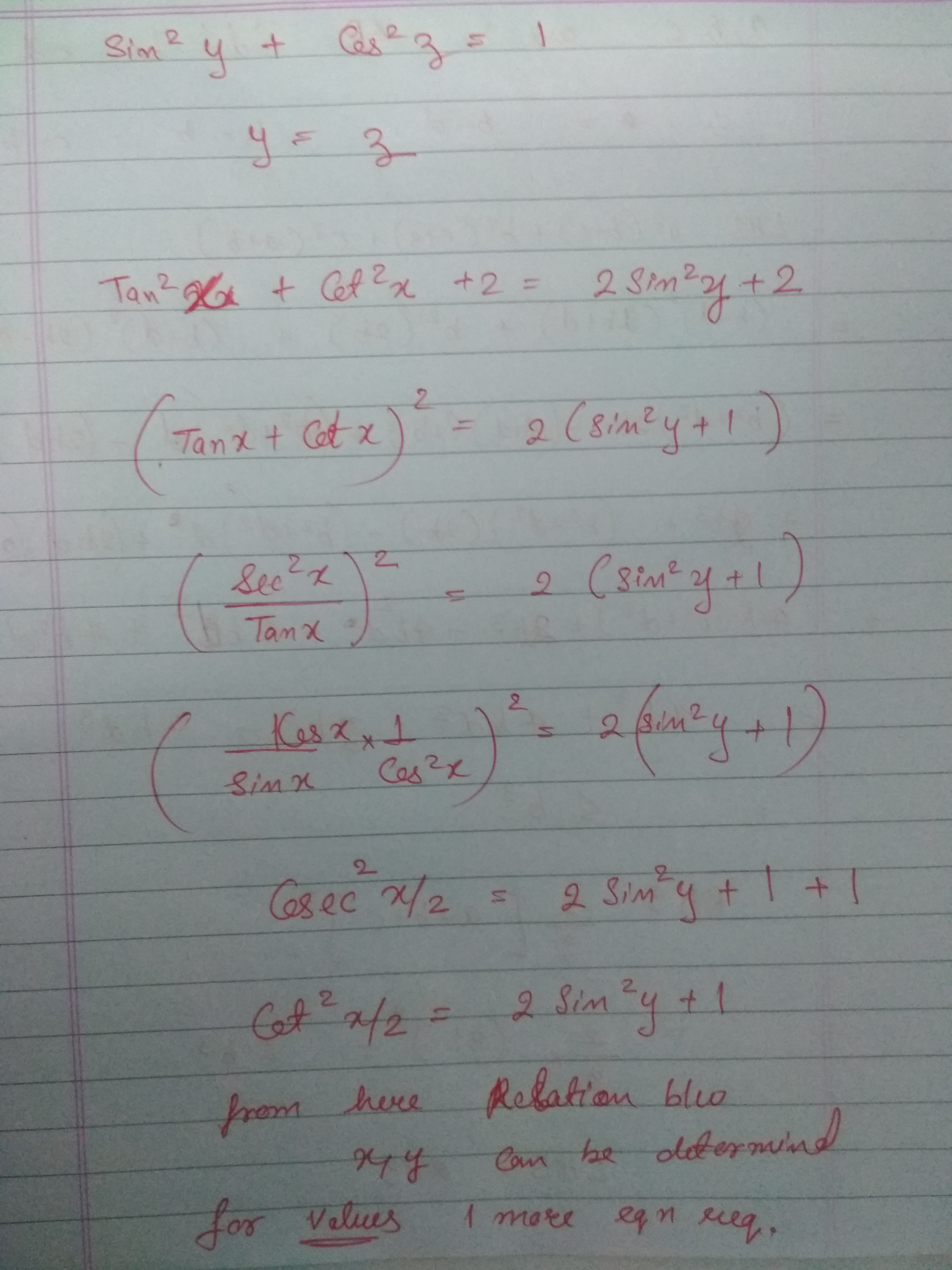



Solve For X Y And Z If Tan 2x Cot 2x 2sin 2y And Sin 2y Cos 2z 1 Askiitians



Http Www Mayfieldschools Org Downloads 4 8 double angle formulas key Pdf



If Sin 3x Cos X Then Find Tan 2x Quora




If Cos X Y 4 5 Sin X Y 5 13 And X And Y Lies Between 0 And P 4 Then What Is The Value Of Tan2x Quora




Find A Sin 2x B Cos 2x And C Tan 2x If Cos X Chegg Com



2




Math34 Trigonometric Formulas




Answered Tan X Sin X Sin X Cos X Sin X Cos Bartleby
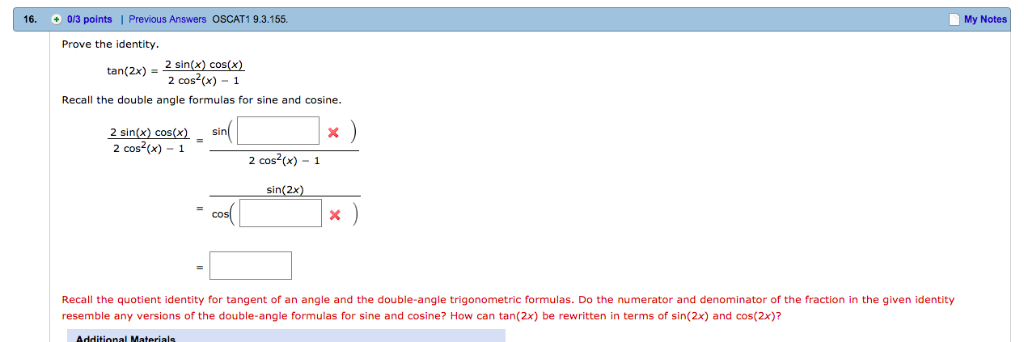



16 0 3 Points Previous Answers Oscat1 9 3 155 My Chegg Com




How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic




Double Angle Properties Rules Formula Examples Video Lesson Transcript Study Com



Tan2x ただの悪魔の画像




Misc 8 Tan X 4 3 Find Sin X 2 Cos X 2 And Tan X 2




Multiple Angle Formulas Es Demonstrating Understanding Of Concepts Warm Up Use A Sum Formula To Rewrite Sin 2x In Terms Of Just Sin X Cos X Do Ppt Download



Derivatives Of Trigonometric Functions




Problem 4 Using The Sin And Cos Addition Formulas Chegg Com
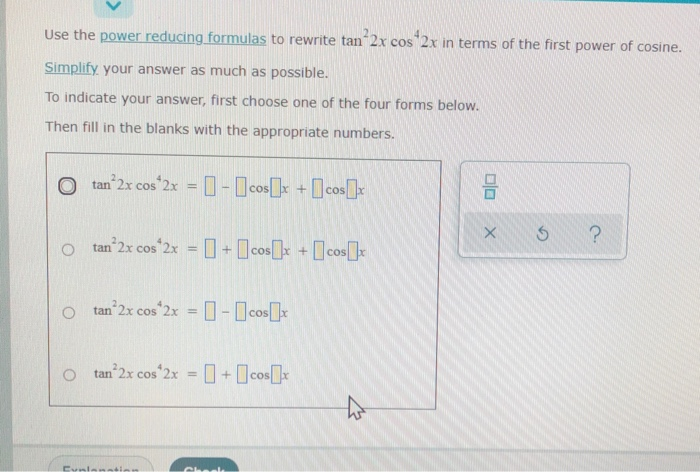



Use The Power Reducing Formulas To Rewrite Tan 2x Cos Chegg Com



1




How Do You Solve 1 Tan 2x 6 2sec 2x Socratic




5 5 Multiple Angle And Product Sum Formulas Find All Solutions In Ppt Download




Lesson 4 5 Double Angle Formulas




Example 28 If Tan X 3 4 Find Sin X 2 Cos X 2 Tan X 2




Example 22 Solve Tan 2x Cot X Pi 3 Teachoo Examples



Prove Sin2x 2tanx 1 Tan 2x Socratic
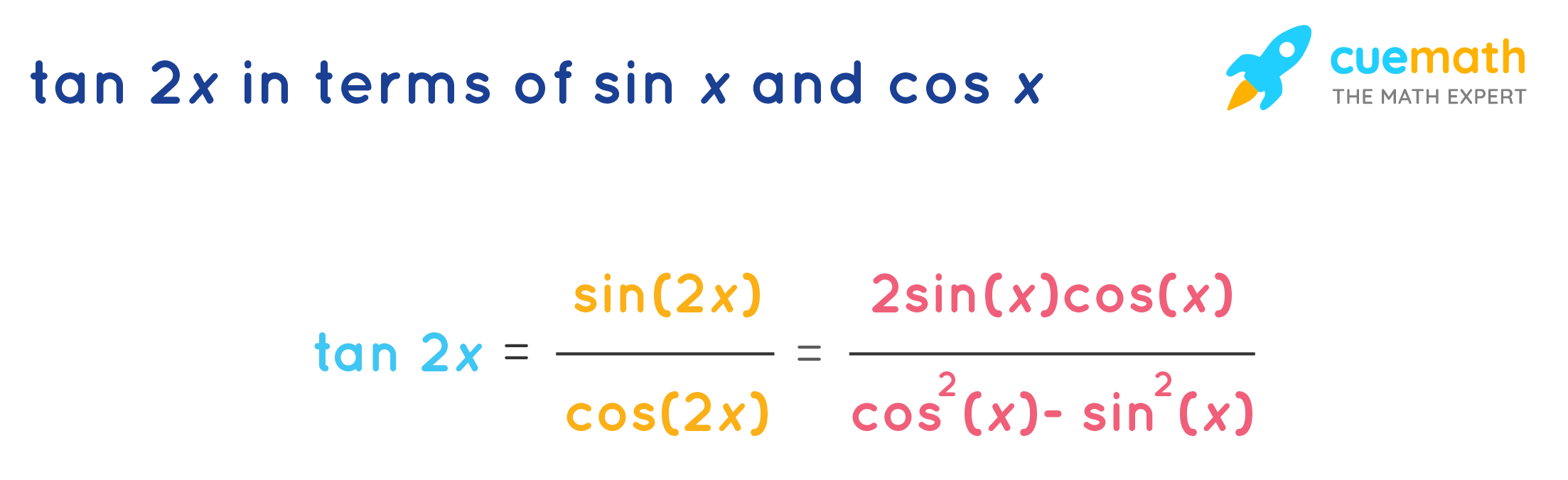



Tan 2x Formula What Is Tan 2x Formula Examples




Solve The Trigonometric Equation Tan X Tan 2x Tan X Tan 2x 1




How To Write Double Angle Formula Sin 2x In Terms Of Tan X Youtube




How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic




Section 7 3 Double Angle Half Angle And Chegg Com




What Is Integral Of Sin2x Tan2x Quora




Multiple Angle Formulas Es Demonstrating Understanding Of Concepts Warm Up Use A Sum Formula To Rewrite Sin 2x In Terms Of Just Sin X Cos X Do Ppt Powerpoint




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo
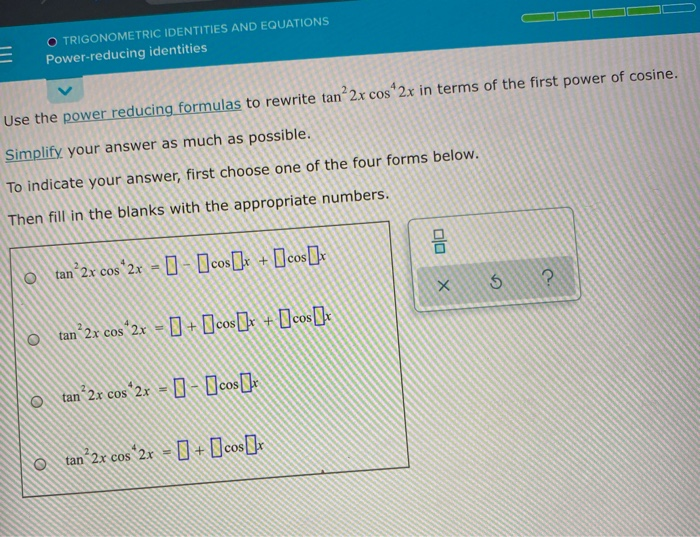



O Trigonometric Identities And Equations Chegg Com



If T Tanx How Can One Express Cosx 2 In Terms Of T Quora




Tan2x Sin2x Tan2x Sin2x 5 1 Brainly In




Ppt Multiple Angle Formulas Ts Making Decisions After Reflection And Review Powerpoint Presentation Id



What Are The Formulas Of Cos 2x Quora




Lesson 24 Double Angle Half Angle Identities Ppt Video Online Download




Section 7 3 Double Angle Half Angle And Sum




Trigonometric Identity With Pythagorens Sec 2x Sin 2x Cos 2x Tan 2x Youtube




Expressing Sin X And Cos X In Terms Of T Tan X 2 Youtube



3




Use The Power Reducing Formulas To Rewrite Tan 2x Chegg Com




Find The Range Of F X Sqrt 4 Sqrt 1 Tan 2x




Cos X Plus Sin X Upon Cos X Minus Sin X Minus Cos X Minus Sin X Upon Cos X Plus Sin X Is Equal To 2 Brainly In




Cosx 3 5 Find Tanx 2 Half Angle Tangent Formula Derivation With Important Example Youtube




Calculate Sin2x Cos2x And Tan2x For Given Tanx In Quadrant 2 Youtube




Answered Find Sin 2x Cos 2x And Tan 2x From Bartleby




Sec 1 1 Tan 2x 1 Tan 2 X



1




View Question Find Sin 2x Cos 2x And Tan 2x From The Given Information Tan X 1 2 Cos X 0



Solved A First Rewrite The Left Hand Side 1 Tan 2x In Terms Of Sin X And Cos X B Next Add The Two Terms In The Expression You Got In Part




Ch 6 Review Assignment Key
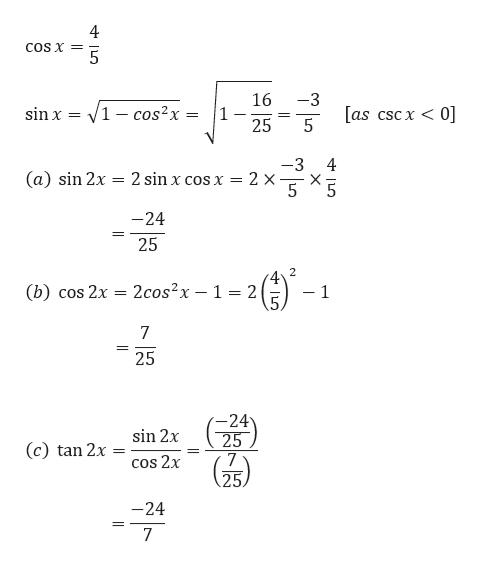



Answered If Cosx 4 5 Cscx 0 Then Sin 2x Bartleby



0 件のコメント:
コメントを投稿